Práce s daty, prokládání a interpolace

Ukážeme si nyní neco snad praktického pro studenty a snad techniky obecne. Casto máme k dispozici nejaká data ve forme tabulky, pro práci však potrebujeme interpolovat mezi zadanými hodnotami nebo dokonce vyjádrit alespon približne závislost dat analyticky. Chceme-li být duslední, musíme dodat, že veškeré interpolace jsou vecí více ci méne dobré víry: prísne vzato nic o chování funkce mimo zadané hodnoty nevíme. V technické praxi však casto již z fyzikální podstaty deje mužeme predpokládat spojitost a obvykle dokonce hladkost uvažované funkce.

Zacneme príkladem. V místnosti rozumné velikosti je vzduch o teplote 20°C, merili jsme soucinitel prestupu tepla mezi stenou a vzduchem pro ruzné teploty steny a výsledky zadali jako 2D List:

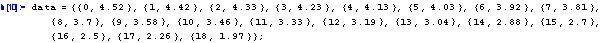
První souradnice je teplota steny a druhá je hodnota soucinitele prestupu tepla samovolnou konvekcí /pro ty, kterí se zabývají sdílením tepla: sálání není zahrnuto/ ve wattech na metr ctverecní a kelvin.

Pokud chceme videt prubeh funkce a stací nám pospojování bodu úseckami, použijeme ListPlot:

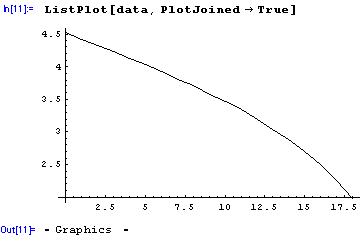
Chceme-li napríklad vycíslit funkci mezi zadanými body, použijeme príkaz Interpolation:

S funkcí "alfa" mužeme pracovat obvyklým zpusobem. Mužeme ji napríklad derivovat, integrovat, tisknout, použít na pravé strane diferenciální rovnice a podobne. Pozor ovšem, bude-li argument mimo rozsah nezávisle promenné v tabulce, s nejvyšší pravdepodobností obdržíme blud:

Naštestí nás M. na fakt, že jsme mimo rozsah platnosti interpolace a že extrapoluje, upozorní. Príkaz Interpolation[data] interpoluje prubeh mezi body polynomem tretího stupne; potrebujeme-li napríklad druhý stupen, napíšeme Interpolation[data,InterpolationOrder->2].

Hledání analytické náhrady funkce zadané tabulkou

V predchozím jsme vytvorili interpolacní funkce, která procházela presne zadanými body /v kartézských souradnicích body (x,y) z tabulky/ a mezi nimi interpolovala polynom zvoleného stupne. V následujícím nahradíme funkci z tabulky lineární kombinací zvolených funkcí, vetšinou tato náhrada již zadanými body procházet presne nebude, ale napríklad bude respektovat jiné požadavky. Pochopitelne kvalita náhrady záleží velmi na tom, jak uhodneme funkce z nichž lineární kombinaci vytváríme. Nekdy je vodítkem treba fyzikální zákonitost, jindy se na graf /získaný napríklad LitPlotem/ díváme tak dlouho, až nás neco napadne.

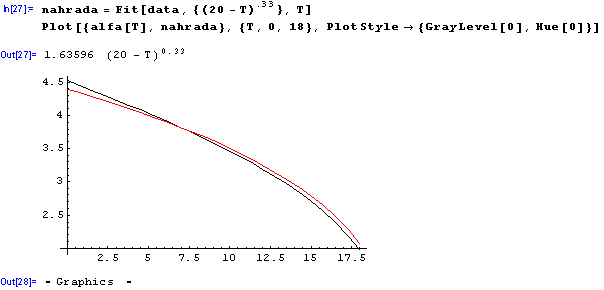
Ted jsme vuci tem, kterí se sdílením tepla nezabývají trošicku nefér, vytáhli jsme králíka z klobouku a nevysvetlili jak. Zkusme to ješte jednou a s komentárem:

Syntaxe je Fit[data,{funkce tvorící bázi lineární náhrady, strucne to, cím prokládáme},nezávisle promenná] Náhrada spocívá v nalezení císel a,b,c,d tak, aby výraz

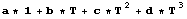
byl co možná nejlepším proložením zadané tabulky ve smyslu minimální kvadratické odchylky /nejmenších ctvercu/, tedy aby výraz

byl minimální. Scítání probíhá pres všechny body v tabulce data.

Dalším zpusobem aproximace dat z tabulky je použití príkazu NonlinearFit. Jde o príkaz z package /Add-ons->Standard Packages-> Statistics->NonlinearFit/ NonlinearFit. Nejprve nacteme package:

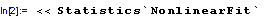
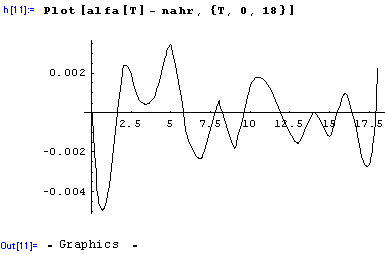
A vidíme, že náhrada je velmi dobrá, je to dáno tím, že jsme /odjinud-zde z teorie sdílení tepla konvekcí/ znali tvar závislosti, model, v nemž nám M. urcila hodnoty konstant.

Syntaxe je: NonlinearFit[data, model s obecnými parametry, nezávisle promenné, parametry].

Náš model byl

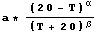
nezávisle promenná T, parametry, které mají být urceny jsou . Protože jich je více, tvorí List, jsou ve složených závorkách.

notebook 2.01

Přílohy

image002.gif		1390 bytes
image004.gif		1864 bytes
image006.gif		753 bytes
image008.gif		1133 bytes
image010.gif		3166 bytes
image014.gif		355 bytes
image016.gif		667 bytes
image018.gif		484 bytes
image020.gif		1328 bytes
image022.gif		2660 bytes
image024.gif		368 bytes