-- Josef Čapek
■ Pískoviště
■ Poslední změny
■ Registrace
■ Etický kodex
■ Nápověda
■ Administrace
■ Hlášení chyb
 |  |
© 1999-2008 HEAT

| Začínáme s Mathematica-ou ... díl 6. |
Solve II.
Dále již budeme stručnější: postupně pronikáme do logiky M. a tak si to můžeme dovolit.
Příkaz NSolve má syntaxi NSolve[rovnice,proměnná]
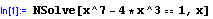
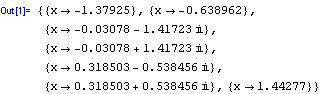
A je určen k řešení polynomiálních rovnic. Při transcendentních rovnicích řešení nalezeno není:
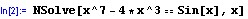

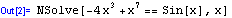
V tuto chvíli je na místě otázka rozdílu mezi příkazy FindRoot a NSolve. Pokud je problém polynomiální, příkaz NSolve najde všechna komplexní řešení, navíc nemusím omezit obor hodnot proměnné, kterou hledám.
Pokud se v rovnici argumentu příkazu FindRoot nevyskytuje formálně komplexní číslo /Mathematica považuje číslo 1 za reálné a číslo 1+0*I za číslo komplexní/, obdržím 1 reálný kořen.
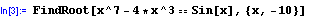

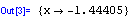
Příkaz LinearSolve[matice,vektor pravých stran] řeší maticovou rovnici matice*x=vektor pravých stran

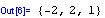
Úloha pro zvídavého čtenáře: Čím je tato soustava zvláštní? Má takto konstruovaná soustava vždy celočíselné řešení?
Zároveň jsme se naučili syntaxi jednoho způsobu zadávání matic.

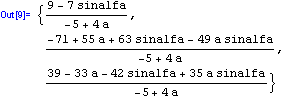
Vidíme, že řešení je v symbolickém tvaru.
Příkaz MainSolve[...] slouží k sofistikovanějším operacím se soustavami lineárních rovnic /eliminace vybraných proměnných, transformace do jiných proměnných a podobně.
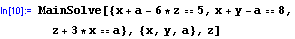
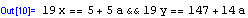
Čili ze soustavy rovnic chceme vyjádřit vztah mezi proměnnými x,y,a, proměnná z se ve výsledku nemá vyskytovat. Takto kladený požadavek není vždy splnitelný, v tom případě se stává příkaz MainSolve[..] funkcí typu boolean s hodnotou False.
Podívejme se dále na příkaz DSolve. Jsme již zkušenější a nepotřebujeme příklad. Umíme používat nápovědu...čili:
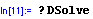

Tak to zkusíme, ne? Ale jak zapsat derivaci...jasně, derivace je anglicky derivative. Jestli tenhle přikaz v M. existuje, bude začínat velkým písmenem; to už víme.


Takže vidíme, že pro začátek vystačíme s čárkou. Což takhle elektrický obvod:
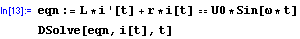
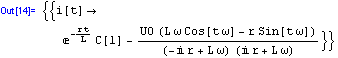
A vida! Máme obecné řešení. Kdybychom chtěli, aby i[0]==i0 ...už umíme, aby M. pracovala s více objekty, jako s jedním: použijeme složené závorky!
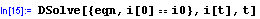
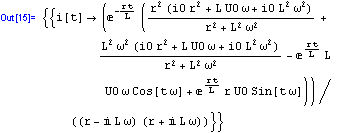
A vidíme, nebolelo to.
O poslední při příkazy zůstanete ochuzeni; poslední je systémový a podle mého názoru neužitečný... koneckonců umíte používat help, ne?
Zastavme se ještě u příkazu NDSolve. Už víme, nebo tušíme, že to bude příkaz k řešení /Solve/ diferenciálních /D/ rovnic a toto řešení bude numerické /N/.
/Analyticky řešitelných diferenciálních rovnic je nejvýše alef jedna, celkem je diferenciálních -rozuměj obyčejných diferenciálních rovnic konečného řádu- alef dva. Tedy téměř žádné diferenciální rovnice nejsou analyticky řešitelné; příkaz NDSolve nám pomůže se řešení přiblížit./
WARNING: Jde o numeriku; řešení samo existovat nemusí /podaří-li se vám zadat pravou stranu jako nespojitou funkci ve více než konečném počtu bodů/, nemusí být jediné /nesplníte-li Lipschitzovu podmínku/; přesto vám numerické metody nějaké řešení obvykle nabídnou. S řešením dané rovnice toto řešení nemusí mít nic společného. Mathematica je inteligentní systém; potřebu inteligence uživatele však eliminovat neumí.
Takže pro začátek zkusíme rovnici u níž řešení známe. A zároveň si napíšeme "prográmek" v Mathematice.
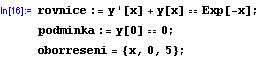
rovnice je samotná diferenciální rovnice, podminka je její okrajová podmínka.
Protože budeme chtít výsledek vytisknout přes celý obor řešení, tento obor si zadefinujeme.

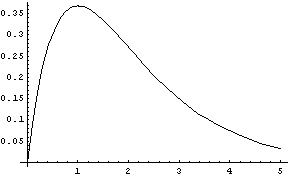
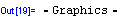
Příkaz NDSolve vytvoří interpolační funkci; ta má strukturu datovou a nelze s ní jednoduše pracovat. Proto příkazem
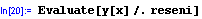
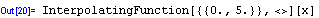
vytvoříme "tisknutelnou" funkci. Příkaz Evaluate[oborreseni]
způsobí, že příkaz Plot dosadí za objekt oborreseni hodnotu {x,0,5}.
Pokud je vám tento prográmek jasný, je vše v pořádku. Pokud ne, zkuste si projít a provést jednotlivé příkazy postupně, bez středníků, abyste viděli výsledky. pokud chcete "vidět" proměnnou definovanou pomocí SetDelayed, jednoduše si ji necháte zobrazit vypsáním jejího označení na další řádek a vyhodnocením onoho řádku:
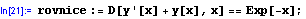

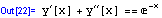
Takto později budete tvořit programy: nejprve řádek po řádku s vypisováním výsledků, poté rušení jinak zbytečných výpisů a sdružování příkazů do větších celků.
Přílohy
| index_gr_1.gif |  |
348 bytes |
| index_gr_10.gif |  |
194 bytes |
| index_gr_11.gif |  |
970 bytes |
| index_gr_12.gif |  |
1058 bytes |
| index_gr_13.gif |  |
642 bytes |
| index_gr_14.gif |  |
367 bytes |
| index_gr_15.gif |  |
202 bytes |
| index_gr_16.gif |  |
1889 bytes |
| index_gr_17.gif |  |
237 bytes |
| index_gr_18.gif |  |
1996 bytes |
| index_gr_19.gif |  |
672 bytes |
| index_gr_2.gif |  |
1316 bytes |
| index_gr_20.gif |  |
845 bytes |
| index_gr_21.gif |  |
424 bytes |
| index_gr_22.gif |  |
1647 bytes |
| index_gr_23.gif |  |
810 bytes |
| index_gr_24.gif |  |
1170 bytes |
| index_gr_25.gif |  |
1165 bytes |
| index_gr_26.gif |  |
224 bytes |
| index_gr_27.gif |  |
354 bytes |
| index_gr_28.gif |  |
481 bytes |
| index_gr_29.gif |  |
473 bytes |
| index_gr_3.gif |  |
400 bytes |
| index_gr_30.gif |  |
194 bytes |
| index_gr_31.gif |  |
279 bytes |
| index_gr_4.gif |  |
848 bytes |
| index_gr_5.gif |  |
375 bytes |
| index_gr_6.gif |  |
470 bytes |
| index_gr_7.gif |  |
767 bytes |
| index_gr_8.gif |  |
245 bytes |
| index_gr_9.gif |  |
889 bytes |
| zacmath6.nb |  |
26035 bytes |
