| Začínáme s Mathematica-ou II... díl 2. |
Práce s daty, prokládání a interpolace ... podruhé
Příkaz TableTento príkaz je u zkušenejších uživatelu M. Nekterí tvrdí, že není potrebí cyklu, na vše stací Table. Jak to funguje, pochopíme nejlépe na príklade. Upozorneme, že výstupem je vždy List
Jedno použití:

Další možnost: iterátor i pocíná od císla 1 a postupuje po prirozených císlech do císla 10 vcetne.
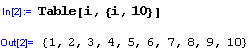
Obdobne iterátor i pocíná od císla 5 a postupuje po prirozených císlech do císla 8 vcetne.
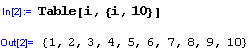
Iterátor pocíná od císla 7 do císla 7,5 s krokem 0,125:
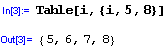
Iterátoru muže být více:
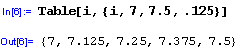
Jak to funguje? Príklad byl zvolen tak, že to lze jednoznacne rozkódovat. Prípadne si s príkazem Table trochu pohrajte. Myslíte-li to s M. aspon trochu vážne, urcite se vám to neztratí.
Vytváret ovšem mužeme i složitejší struktury:
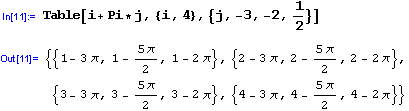
Ukažme si další príklad práce s Table:
Chceme si vytvorit tabulku parciálních derivací soucinu dvou funkcí dvou promenných, tak, že soucet rádu derivací podle x a y je nejvýše 2:
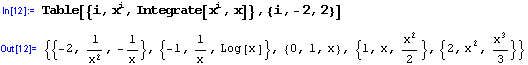
Nyní by nás zajímala substituce za funkce u[x,y] a v[x,y], napríklad:

Aplikujme dosazení na výraz:
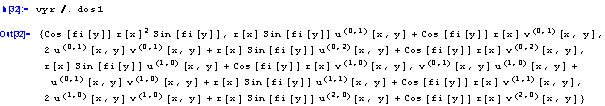
Vidíme, že probehlo dosazení za funkce u[x,y] a v[x,y], nikoli za derivace techto funkcí. Vytvorme si tedy pomocí príkazu Table dokonalejší dosazení:
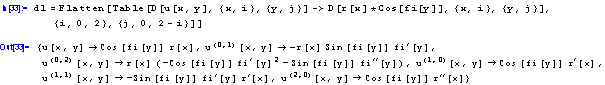
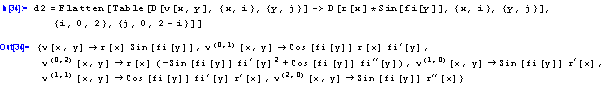
A aplikujme obe dosazení dohromady:
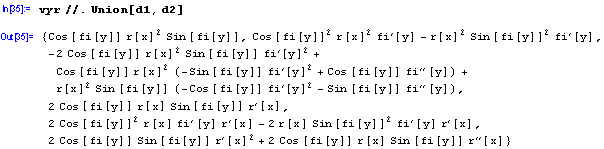
No a kdybychom chteli ony derivace secíst a výraz zjednodušit, mužeme tak ucinit napríklad takto:

notebook 2.02
Přílohy
| image028.gif |  |
693 bytes |
| image030.gif |  |
753 bytes |
| image032.gif |  |
615 bytes |
| image034.gif |  |
816 bytes |
| image036.gif |  |
1739 bytes |
| image038.gif |  |
1585 bytes |
| image040.gif |  |
2707 bytes |
| image044.gif |  |
3006 bytes |
| image046.gif |  |
2256 bytes |
| image048.gif |  |
2255 bytes |
| image050.gif |  |
3525 bytes |
| image052.gif |  |
2078 bytes |