| Začínáme s Mathematica-ou ... díl 7. |
Něco více o funkcích
Než přistoupíme k některým možnostem syntaxe zadávání funkcí, seznámíme se s několika užitečnými instrukcemi; bude to především příkaz Clear[function] a syntaxe logických výrazů.
Příkaz Clear[symbol] vymaže definici symbolu. Tak jako jsou při výpočtech číslovány vstupy a výstupy a je možno je možno je /pomocí nám již známé syntaxe užívající %/ používat, mohlo by se stát, že jsme například před hodinou při práci s jiným programem v M. zadefinvali nějakou funkci /nebo výraz/ pod stejným jménem, což by mohlo vést k omylům a chybám. Doporučujeme tedy před zadefinováním nové funkce použít příkaz Clear. Použití tohoto příkazu ukážeme na příkladě.
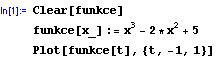
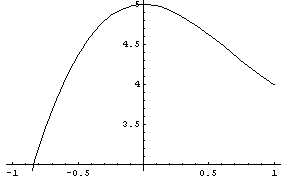
Z didaktických důvodů jsme použili při tisku označení nezávisle proměnné písmeno t a nikoli x; pro námi zadefinovanou funkci není podstatné, jaká je hodnota proměnné x kdesi jinde v programu -pokud se tam vůbec proměnná takto označená vyskytuje-, ale hodnota argumentu v hranatých závorkách. Zde je zřejmý důvod, proč v definicici funkce jsou její nezávisle proměnné označené podtržítkem; za hodnotu proměnné např. x v definici funkce označené x_ se dosazuje při vyčíslování hodnoty funkce číslo uvedené v argumentu funkce, za hodnoty proměnných, které nejsou při definování funkce podtržítkem označeny se berou hodnoty stejně označených proměnných odjinud z programu.
Například:
-ujišťujeme se, že žádná funkce označená písmenem g nemůže kolidovat s námi zamýšlenou funkcí
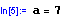
-definujeme konstantu a, kterou využijeme v definici funkce g
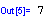
- odpověď M. na definici konstanty a
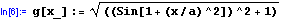
- definujeme funkci g; nezávisle proměnná je x, neboť je na levé straně definice označena podtržítkem; konstanta a je brána jako globální, předtím v programu určený - definovaný či vypočtený - objekt takového typu, že jej lze dosadit do pravé strany definice funkce g / v tomto případě -obecně komplexní- číslo/.
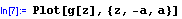
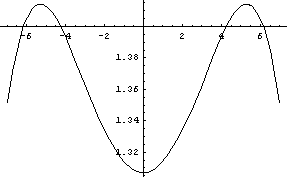
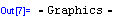
Při tisku se pro výpočet hodnot dosazuje za a v definici funkce výše v programu zadefinovaná hodnota konstanty a a do pravé strany definice funkce se dosazují za nezávisle proměnnou v této definici označenou x hodnoty proměnné z, přičemž tato proměnná z probíhá interval <-a; a>.
Co se stane, když použijeme na místě globální proměnné v definici funkce proměnnou, která nebyla definována si ukážeme opět na příkladu.
- mažeme předchozí /eventuální/ definice symbolu g
- mažeme předchozí /eventuální/ definice symbolu a
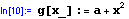
- definujeme funkci g
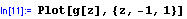




A dostáváme rozličná chybová hlášení - M. nemůže za a nic dosadit; narozdíl od některých jiných SW M. nedosazuje za nedefinované symboly nulu.
Zkusme jiný příklad; proměnná a bude definována až při vlastním tisku:
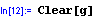
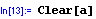
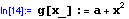
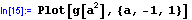
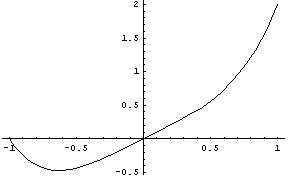
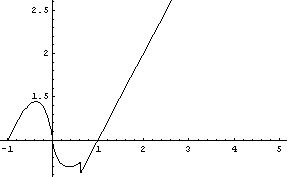
Otázka pro zvídavého čtenáře: jakou funkci jsme vlastně vytiskli?
Pokud jste tuhle otázku zodpověděli správně /přesvědčit se můžete například tím, že vytisknete svoji odpověď a porovnáte ji s daným grafem/, máte v pojmech "argument funkce", nezávisle proměnná", globální konstanta" jasno a můžeme postoupit dále.
Obzvláště v technické praxi nevystačíme obvykle s elementárními funkcemi, ale potřebujeme zadefinovat funkci pomocí různých předpisů na různých intervalech, nebo v závislosti na nějaké podmínce. Syntaxe je následující:
funkce[nezávisleproměnná_]:=výraz1/;podmínka1
funkce[nezávisleproměnná_]:=výraz2/;podmínka2
a tak dále., za poslední podmínkou je středník. A opět příklad přímo z M.:
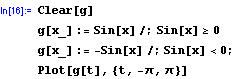
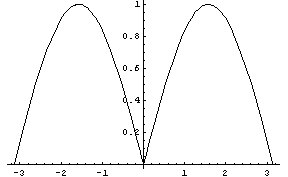
Podmínka i funkce mohou ovšem obsahovat i globální proměnnou:
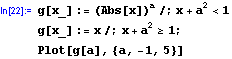
Všimněme si nyní toho, že funkce g je zadefinovaná pro jakýkoli reálný argument; právě jedna ze dvou uvedených podmánek má hodnotu True. Pro takové situace lze s výhodou použít příkaz If.
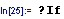

Příkaz If[podmínka,výstup1,výstup2] znamená, že v případě, že má podmínka hodnotu True je výstupem výstup1 a v případě, že má podmínka hodnotu False výstup2. Definice funkce g pak vypadá následovně:
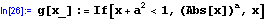
A Abychom se přesvědčili, že jde o "tutéž" funkci, provedeme stejný tisk:
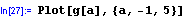
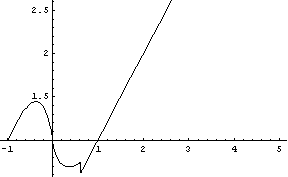
V technické praxi se často vyskytne potřeba komplikovanějších podmínek. Protože podmínka sama je výraz typu boolean, uvedeme zde nějaké operace s objekty tohoto typu. Připomeňme, že výraz typu boolean nabývá nejvýše dvou hodnot a to True a False.

