Symetrizace 1f a 3f spotřebičů
5.10.2002V mnoha průmyslových aplikacích se setkáváme s velkými zařízeními připojenými na síť elektrické energie. Tyto spotřebiče by měly být symetrické, neboť přenos výkonu v tomto stavu způsobuje nejnižší činné ztráty. Proto provádíme tzv. symetrizaci spotřebiče, t.j. naším cílem je vytvořit celek, který bude zatěžovat všechny fáze rovnoměrně; samozřejmým požadavkem je, aby se procesem symetrizace nezvýšil dosavadní činný výkon spotřebiče. To, jak uvidíme dále, se nám podaří vhodnou kombinací indukčnosti a kapacity, které připojíme mezi jednotlivé fáze našeho spotřebiče. Symetrizace se může provádět nejen u stávajících 3f zařízení, ale i u 1f zařízení, které je nutno napájet třemi fázemi. To se využívá hlavně pro napájení energetických zařízení velkých výkonů - nad 500 kW.
Začneme však nejprve reálnou admitancí, například G = 5 S:
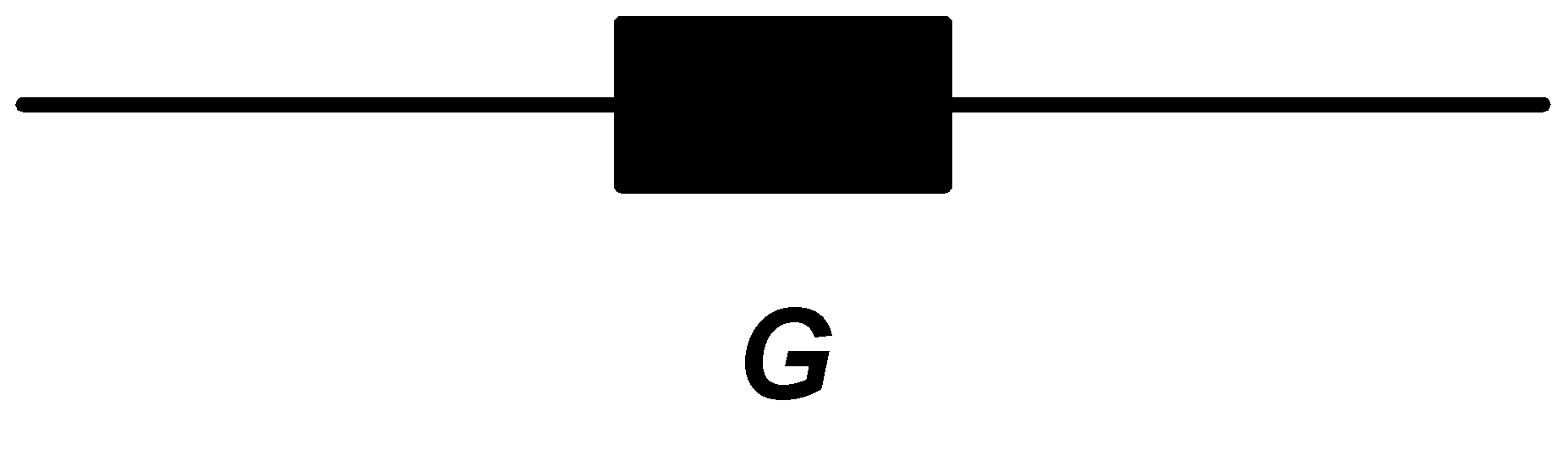 |
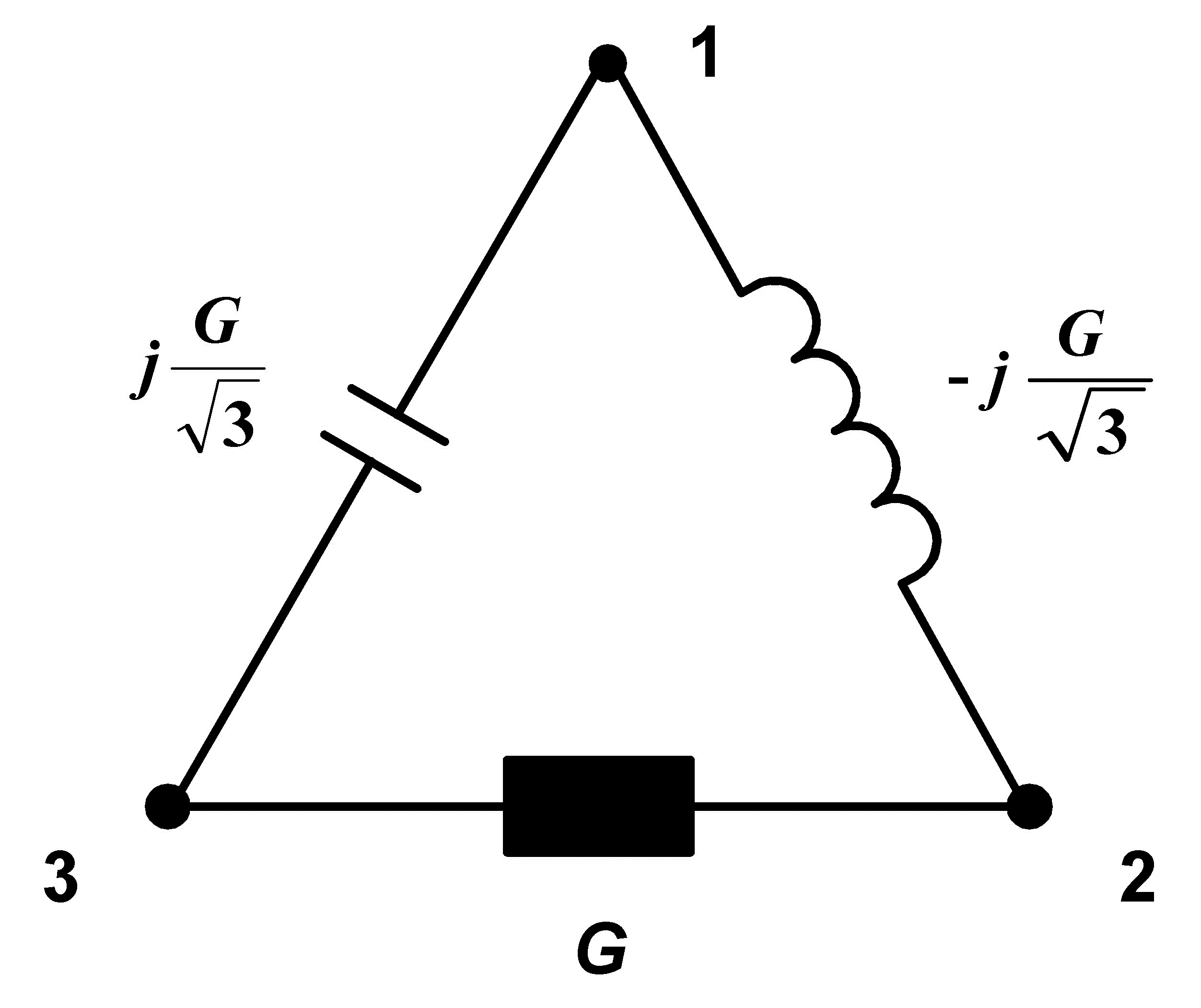
Z ní uděláme symetrickou 3-fázovou reálnou zátěž takto:
 |
Odvození:
Uvažme zapojení obvodových prvků, označení a orientaci obvodových veličin podle schematu:
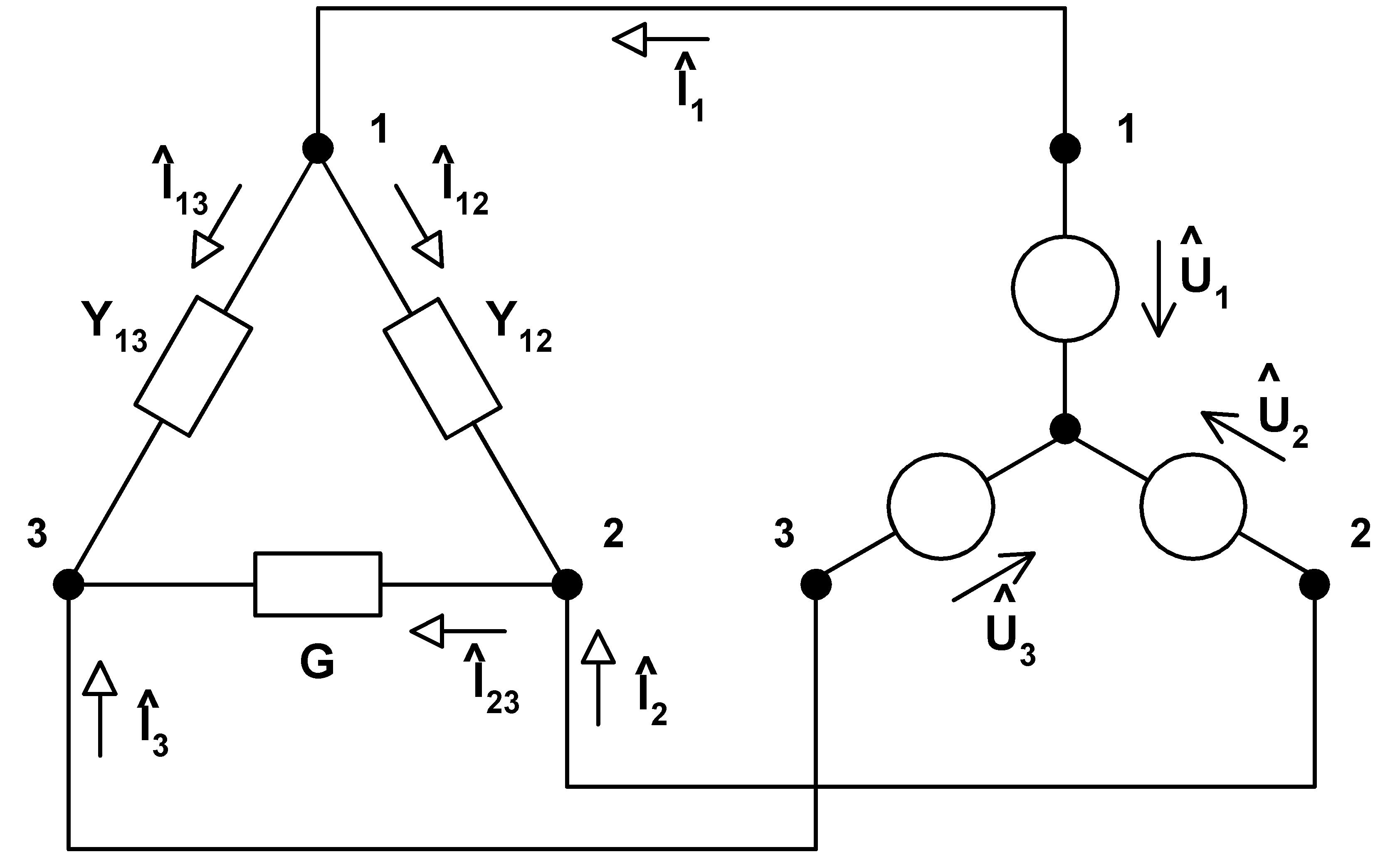 |
Mezi uzly 2 a 3 nechť je zapojena reálná zátěž o vodivosti G (S). Požadujeme, aby po připojení admitancí
Y12 (S) a Y13 (S) byla zátěž reálná a symetrická; dalším požadavkem je, aby
činný výkon odebíraný zátěží zůstal nezměněn, matematizujme tyto požadavky:
# zachování činného výkonu: Y12 a Y13 jsou ryze imaginární,
# výsledné zapojení neodebírá jalový výkon: Y12 = -Y13; položme Y12 = j.Y, Y13 = -j.Y,
# symetrie odebíraných proudů: I1 = k.U1, I2 = k.U2, I3 = k.U3.
Zaveďme označení fázových napětí v elektroenergetice obvyklým způsobem:
U1 = U, U2 = U.a2, U3 =
U.a, kde 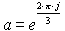 je operátor otočení v komplexní rovině o
je operátor otočení v komplexní rovině o 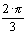 proti směru hodinových ručiček, přestože to řešení
nevyžaduje, je výhodné položit
proti směru hodinových ručiček, přestože to řešení
nevyžaduje, je výhodné položit 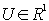 , což jistě můžeme, znamená to jen volbu počátku
měření času při přechodu od fázorů do časové oblasti.
S uvážením těchto podmínek platí:
, což jistě můžeme, znamená to jen volbu počátku
měření času při přechodu od fázorů do časové oblasti.
S uvážením těchto podmínek platí:
I1 = I12 + I13 = j.Y.(U1 -
U2) - j.Y.(U1 - U3) = j.Y.U.(1 -
a2) - j.Y.U.(1 - a) = k.U1 = k.U
I2 = I23 - I12 = G.(U2 -
U3) - j.Y.(U1 - U2) = G.U.(a2
- a) - j.Y.U.(1 - a) = k.U2 = k.U.a2
I3 = -I23 - I13 = -G.(U2 -
U3) - (-j.Y).(U1 - U3) =
-G.U.(a2 - a) + j.Y.U.(1 - a) = k.U3 =
k.U.a
U, a, G jsou zadané veličiny, Y, k neznámé. Máme tedy 3 rovnice pro 2
neznámé, rovnice jsou ovšem lineárně závislé: součet levých stran je nulový na první pohled a pro součet pravých
stran platí:
k.U.(1 + a2 + a) = 0, neboť platí 1 + a2 + a = 0.
Řešení soustavy je ve formě notebooku ,
výsledkem je: k = G a Y = -G /
,
výsledkem je: k = G a Y = -G / .
.
Vidíme, že úloha je splněna: proudy jsou G násobkem příslušných fázových napětí, navíc -podle
předpokladu- 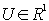 . Celkový činný výkon je:
. Celkový činný výkon je:
P = Re{U.G.U} + Re{a2.U. (a2.U.G)* } = U2
.G.(1 + a2.(a2)* + a.a*) = U2.G.(1 + |a2|2 + |a|2) = U2.G.(1 + |a|4 + |a|2) = U2.G.(1 + 1 + 1) = 3.U2.G
Činný výkon původního zapojení před připojením symetrizačních členů byl: P = G.( .U)2 = 3.U2.G.
.U)2 = 3.U2.G.
Konec odvození.
Stačí tedy zapojit mezi uzly 1-3 ideální kapacitu o velikosti admitance
5 / S (Siemens) a mezi uzly 1-2 ideální
indukčnost o velikosti admitance 5 /
S (Siemens) a mezi uzly 1-2 ideální
indukčnost o velikosti admitance 5 / S,
a dostaneme z jednofázového spotřebiče trojfázový symetrický spotřebič.
S,
a dostaneme z jednofázového spotřebiče trojfázový symetrický spotřebič.
Nyní se však podívejme na obecnou 3f nesymetrickou zátěž. Zesymetrizujeme ji obdobným postupem jako u jedné reálné admitance (viz výše), a to tak, že postupně budeme aplikovat stejný postup symetrizace pro jednotlivé větve zvlášť. Využijeme skutečnosti, že paralelní spojení trojfázových symetrických reálných zátěží se chová jako symetrická reálná trojfázová zátěž. Navíc označení fází čísly 1,2,3 je libovolné při zachování jejich sledu, můžeme tedy při myšleném přečíslování fází postupovat u každé mezifázové zátěže obdobně, jak je uvedeno výše. Vše si nejlépe vysvětlíme na příkladu. Máme takový případ:
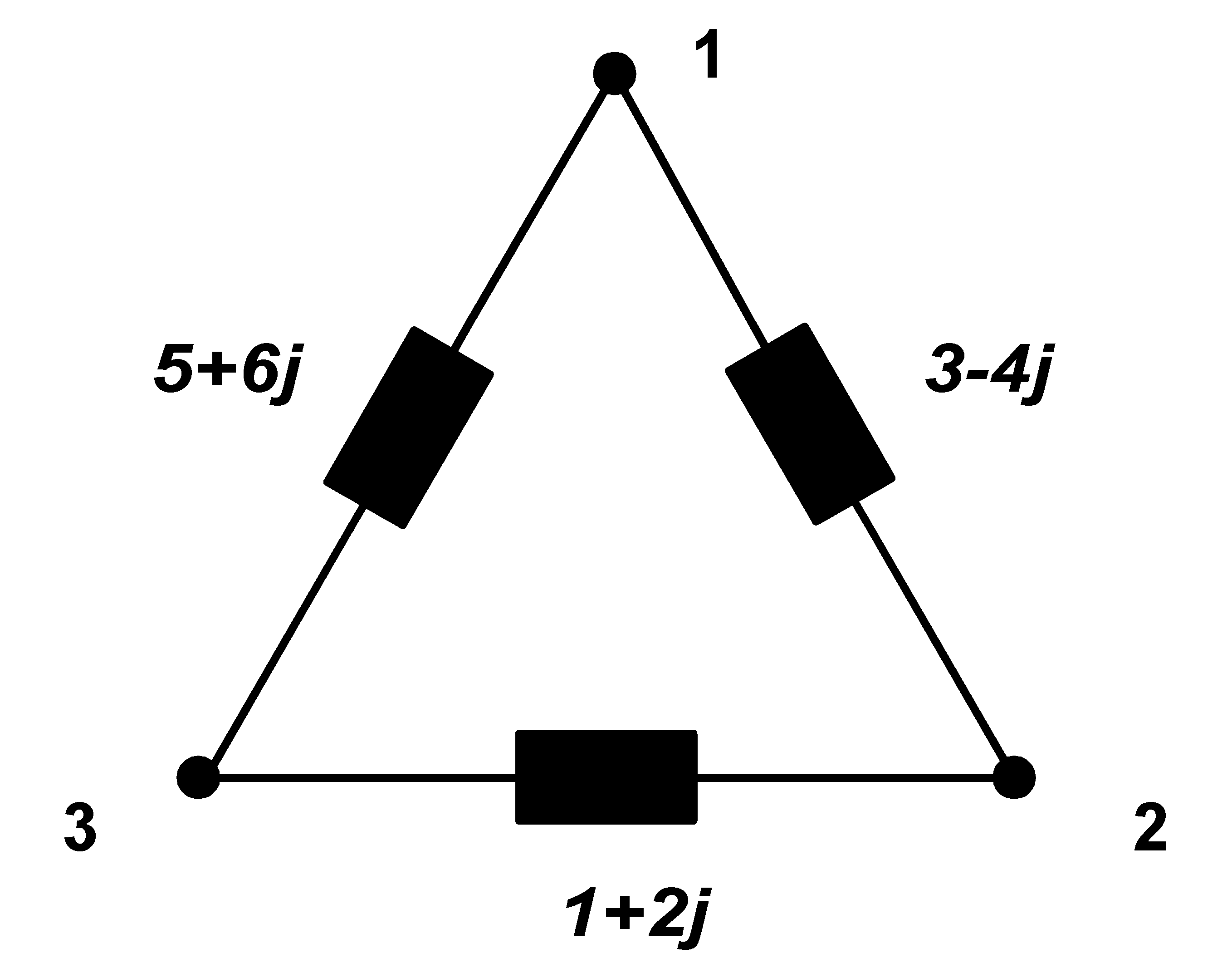 |
Nejprve dosáhneme reálné zátěže mezi jednotlivými uzly, t.j. mezi uzly 1 a 2 připojíme admitanci 4j S, mezi uzly 2 a 3 admitanci -2j S a mezi uzly 3 a 1 admitanci -6j S. Vše přehledně zapíšeme do tabulky.
| větev 1-2 | větev 2-3 | větev 3-1 | |
|---|---|---|---|
| 4j | -2j | -6j | vykompenzováno |
Nyní je obvod vykompenzován, ale ještě ne zesymetrizován:
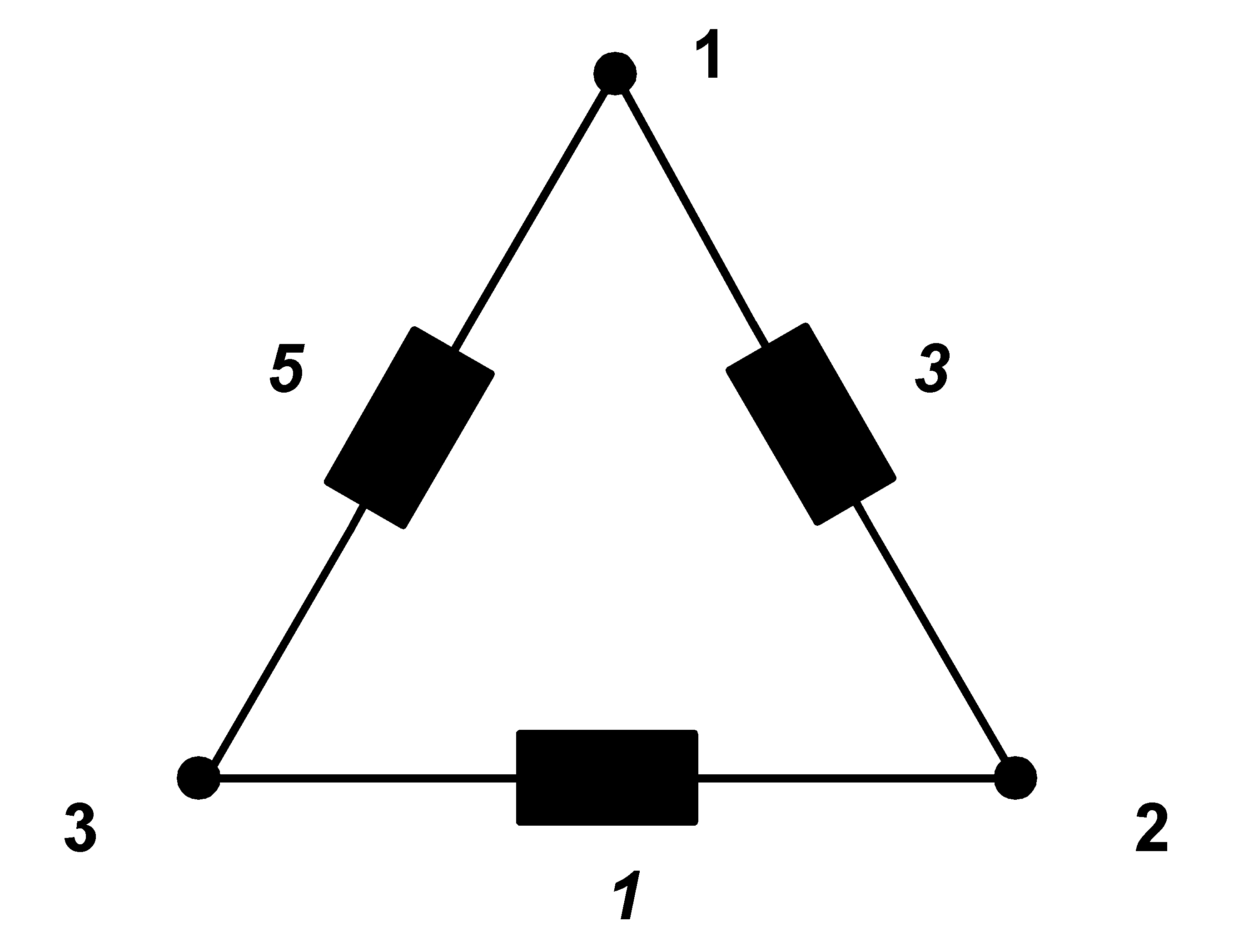 |
Postupme dále. Tento vykompenzovaný obvod považujeme za paralelní spojení třech jednoduchých jednofázových spotřebičů (jsou ale pokaždé mezi dvěma různými uzly),
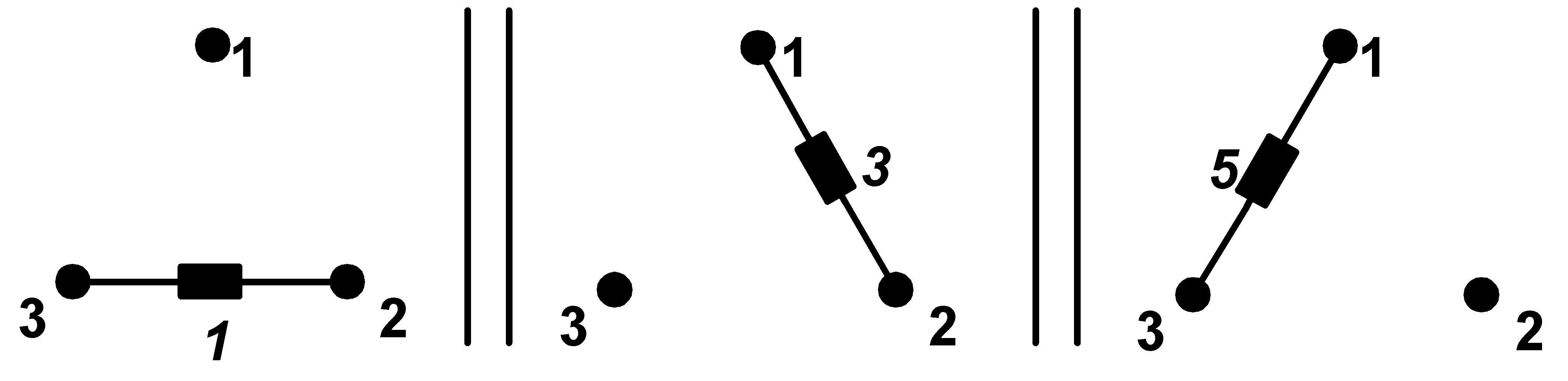 |
a s těmito oddělenými jednoduchými admitancemi provedeme symetrizaci,
jako na začátku, každou admitanci zesymetrizujeme zvlášť.
Pokud provádíme symetrizaci spotřebiče
mezi uzly 1-2, pak mezi uzly 2-3 bude kapacita o velikosti admitance
3 / a mezi uzly 3-1 bude indukčnost o velikosti admitance 3 /
a mezi uzly 3-1 bude indukčnost o velikosti admitance 3 / .
Pro symetrizaci spotřebiče, který je zapojen mezi uzly 3-1, platí analogický postup.
Zkráceně řečeno, schema natáčíme vždy tak, aby se admitance G kryla s požadovanou
admitancí z paralelní kombinace, kterou právě symetrizujeme,
a zbývající větve dopočítáme podle schematu. Natočení totiž nemění sled fází. Pokračujeme dále v tabulce:
.
Pro symetrizaci spotřebiče, který je zapojen mezi uzly 3-1, platí analogický postup.
Zkráceně řečeno, schema natáčíme vždy tak, aby se admitance G kryla s požadovanou
admitancí z paralelní kombinace, kterou právě symetrizujeme,
a zbývající větve dopočítáme podle schematu. Natočení totiž nemění sled fází. Pokračujeme dále v tabulce:
| větev 1-2 | větev 2-3 | větev 3-1 | |
|---|---|---|---|
| 4j | -2j | -6j | vykompenzováno |
-1j/ | 1j/ | příspěvky větví ze schematu | |
3j/ | -3j/ | příspěvky větví ze schematu | |
| 5j / | -5j/ | příspěvky větví ze schematu | |
| ---- | ---- | ---- | ---- |
j (4 +4/ ) ) | j (-2 -2/ ) ) | j (-6 +2/ ) ) | suma sloupců |
V tabulce je důležitý poslední řádek, který je součtem všech příspěvků v dané
větvi. Tyto hodnoty nám určují typ prvku a jeho velikost,
který připojíme paralelně k odpovídající větvi. Jelikož uvažujeme obvod s jednou frekvencí napětí
a proudů, je možno vždy nahradit paralelní kombinaci indukčnosti a kapacity jedním prvkem, indukčností
či kapacitou podle výsledného znaménka admitance. Upozorněme, že velikosti admitancí jsou funkcemi frekvence,
pro obecný obvod s obecným napájením tato náhrada možná není. Například k větvi mezi uzly 3-1 připojíme
kondenzátor o velikosti admitance j(4 +4/ ) S (kondenzátor, protože výraz
je kladný). Výsledkem je tedy schema:
) S (kondenzátor, protože výraz
je kladný). Výsledkem je tedy schema:
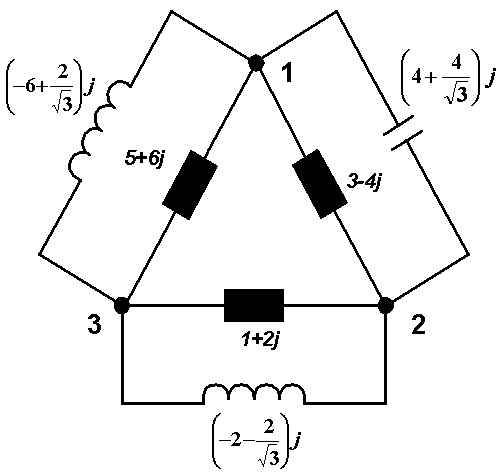 |
Symetrizace byla provedena. Výsledné zařízení odebírá reálný výkon ze sítě. Z libovolné admitance lze tedy vytvořit symetrickou zátěž.
V praxi se ale s explicitním vyjádřením admitance příliš často nesetkáváme. Daleko častější je způsob zadání například:
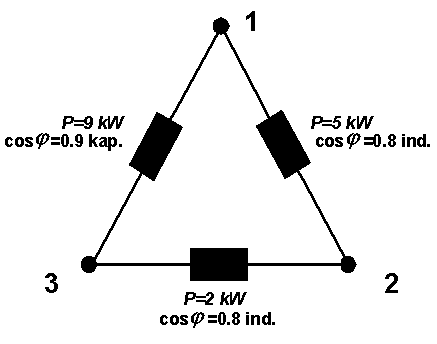 |
Pro získání explicitního vyjádření, na které jsme zvyklí, použijeme následující vzorec, který je ilustrován výpočetem:
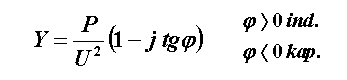 |
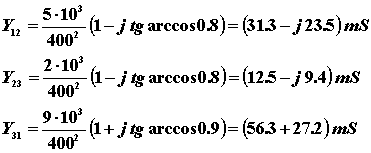 |
Dostali jsme explicitní vyjádření admitance. S těmito hodnotami dále nakládáme, jako v předchozím příkladě.
KONEC ZVONEC.
Přílohy
| Acko.gif |  |
971 bytes |
| Ur.gif |  |
935 bytes |
| Zlomek.gif |  |
904 bytes |
| odvozeni.png |  |
34329 bytes |
| sqrt(3).png |  |
190 bytes |
| sym_1plainG.png |  |
3447 bytes |
| sym_3Gex2_zadani.png |  |
4137 bytes |
| sym_3Gex_paral.png |  |
22302 bytes |
| sym_3Gex_vykomp.png |  |
20068 bytes |
| sym_3Gex_vysledek.png |  |
7241 bytes |
| sym_3Gex_zadani.png |  |
22163 bytes |
| sym_3plainRLCcis.png |  |
37165 bytes |
| sym_vypocet.png |  |
3713 bytes |
| sym_vzorec1.png |  |
1800 bytes |
| symmetrization.nb |  |
4967 bytes |
