-- Serna
■ Pískoviště
■ Poslední změny
■ Registrace
■ Etický kodex
■ Nápověda
■ Administrace
■ Hlášení chyb
 |  |
© 1999-2008 HEAT

| Začínáme s Mathematica-ou ... díl 1. |
Slovo úvodem
Mathematica je jako Prsten moci J.R.R. Tolkiena. Čím větší jsou znalosti uživatele, tím více mu M. může poskytnout. Řekneme-li, že M. umí všechno, nemáme pravdu, ale až zas tak daleko od ní nejsme. Tento fakt je ovšem vykoupen tím, že M. není "plug and play", "user friendly" a tak podobně. K proniknutí -i jen částečnému- do logiky M. je potřebí poměrně dost úsilí a času.
Následující text vyžaduje jen elementární znalost matematiky - tu obsahuje formulace problému, který chceme řešit a analýza získaných výsledků.
V tomto kursu potřebujeme ale pochopení základních pojmů...jak to jen říci: my, lidé, nejsme "tabula rasa", ale máme mnoho "předporozumění"; když si dítě hraje s chřestítkem, zkoumá grupové vlastnosti našeho fyzikálního prostoru; má se za prokázané, že toto zkoumání je v nás hardwarově naprogramováno. Za další život získáme mnoho dalších předporozumění; slovo "kdoule" je pro nás spojeno se všemi situacemi, kdy jsme se se slovem "kdoule" setkali. Toto předporozumnění je z větší části nevědomé.
Mathematica žádné předporozumění nemá. Zkusme tuto situaci demonstrovat na použití znamení rovnosti:
- a=b je výrok, tedy proměnná typu boolean, pokud a a b jsou známé objekty
- x=4 může být oznámení výsledku
- x=4 může být definice konstanty
- x=4 může být definice proměnné pojmenované x do které vkládáme hodnotu 4, implicitae je tedy pro nás x proměnná typu číslo; tak samozřejmé to však není, je myslitelná proměnná, která je buď typu číslo, nebo deštník, nebo rovnice. Slovem proměnná v tomto kursu zásadně rozumím místo v paměti, do kterého mohu uložit jakýkoli objekt smluveného typu. Všechny relace a operace možné s daným typem jsou možné i s těmito místy v paměti.
- x=5*x-8 znamená použití znaménka rovnosti obvykle ve smyslu rovnice k řešení
- atd.atd.
Nejsem teď matematicky přesný; cílem tohoto kursu není vytvoření košer teorie matematických objektů; koneckonců být přesný snad ani možné není; jak říká Hegel: "u podstaty je vše relativní".
Cílem je nyní přivést vás k pochopení složitosti syntaxe M. M. nemá předporozumění a nepozná, který z významů například onoho "rovnáse" máte na mysli. Proto každý z uvedených významů má svou vlastní syntaxi.
- a=b je nová proměnná typu boolean
- x=4 jako výsledek má v M. syntaxi x->4
- x=4 jako přiřazení čísla 4 proměnné x x=4
- x=4 jako definice proměnné, přiřazení hodnoty č proběhne při použití x x:=4
- x=5*x-8 jako rovnice x==5*x-8
- atd.atd.
Obdobně se dále setkáte se závorkami; zkuste se zamyslet, co má použití závorek v zápisu funkce y=f(x) společného s použitím závorek ve výrazu (3+x)*(4-x). Mnoho toho není. Zkuste se zamyslet, co znamená slovo výraz, které jsme tak samozřejmě použili. Zkuste...ale ne, z toho už bolí hlava.
Shrnutí: konvenční zápis není bez předporozumění jednoznačný; symbolům majícím v obvyklém matematickém zápise více významů odpovídají v M. skupiny řetězců znaků tak, aby vyjádření pomocí těchto řetězců bylo jednoznačné. Nebo přesněji: zobrazení mezi syntaxí a sémantikou musí být vzájemně jednoznačné.
A teď už do toho!
1/ Základní HELP: na příkaz ?řetězec M. odpoví helpem týkajícím se řetězce. Platí hvězdičková konvence, tedy ?*Sin dá výstup výpis příkazů s libovolným začátkem končících Sin tedy např. ArcSin, Sin, ale NIKOLI např. Sinh.
Příklad:
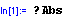
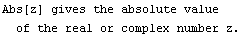
UPOZORNĚNÍ: M. ROZLIŠUJE velká x malá písmena!!!
PRAVIDLO: M. příkazy začínají velkým písmenem; pokud je příkaz vytvořen z více slov, každé začíná velkým písmenem např. LaplaceTransform[ ]
2/ Podrobnější help: příkazem ??řetězec získáme podrobnější informaci o řetězci
3/ Zabudované konstanty: M. má více zabudovaných konstant; pro nás budou nejdůležitější tyto: e označené E, π označené Pi, imaginární jednotka označená I, nekonečno označené Infinity.
PRAVIDLO: Při používání těchto konstant mohu libovolně střídat symboly z palet se slovním vyjádřením /jde o FullForm, StandardForm atd. formáty M.; v tuto chvíli to nebudeme blíže rozebírat/
UPOZORNĚNÍ: Použití konvenčního zápisu pomocí palet není vždy ekvivalentní na první pohled stejnému standardizovanému slovnímu zápisu
4/ Vyčíslení výsledků: M. je SW primárně určený k symbolickým výpočtům; například při sčítání zlomků je výstupem nejprve zlomek, obdobně při operacích s komplexními čísly atd. Chceme-li číselný výsledek, máme následující možnosti:
- Příkaz N[a] poskytne číslo a na pevný počet desetinných míst /např. 6/
- Příkaz N[a,k] poskytne číslo a na k desetinných míst
- Příkaz a//N je stejný jako příkaz N[a]
Jistě si každý povšiml, že výše uvedené příkazy měly své argumenty v hranatých závorkách. To není náhoda, ale pravidlo. V M. je to se závorkami následovně:
Přílohy
| index_gr_1.gif |  |
158 bytes |
| index_gr_10.gif |  |
149 bytes |
| index_gr_2.gif |  |
566 bytes |
| index_gr_3.gif |  |
157 bytes |
| index_gr_4.gif |  |
137 bytes |
| index_gr_5.gif |  |
147 bytes |
| index_gr_6.gif |  |
147 bytes |
| index_gr_7.gif |  |
147 bytes |
| index_gr_8.gif |  |
152 bytes |
| index_gr_9.gif |  |
145 bytes |