-- Montaigne
■ Pískoviště
■ Poslední změny
■ Registrace
■ Etický kodex
■ Nápověda
■ Administrace
■ Hlášení chyb
 | 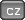 |
© 1999-2008 HEAT

[Back to current version] [Restore this version]
| Mathematica® v el.tep. technice ... díl 1. |
Řešení ustálených 1D tepelných polí.
Základem je Fourier Kirchhoffova rovnice


Pro stacionární případy obdržíme v 1D rovnici pro l závislé na teplotě a souřadnici.
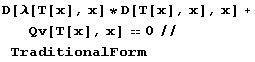
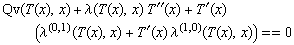
Ukážeme si nějaké základní případy. Začněme nejjednodušším: stěna tloušťky d má tepelnou vodivost l=konst , v x=0 má teplotu T0 a teče jí tepelný tok q [W/(m^2 K)]. Ve stěně teplo nevzniká. Naše rovnice má tvar
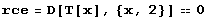
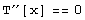
Cauchyho úloha má v tomto případě fyzikální smysl následující:
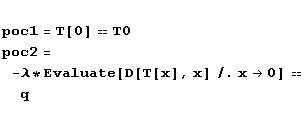
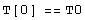

Řešení obdržíme snadno a rychle:


A vidíme lineární závislost teploty na souřadnici. Například pro cihlovou zeď ....
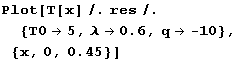
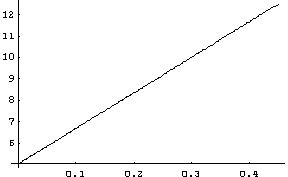
Schválně jsme napsali "Cauchyho úloha" a nikoli "okrajová podmínka". F.-K. rovnice je parciální diferenciální rovnice, okrajová podmínka znamená znalost řešení na hranici nějaké oblasti, při redukci na 1D problém je touto oblastí intarval a jeho hranicí dva jeho krajní body. Ovšem pro obyčejné diferenciální rovnice je třeba znát v jednom bodě hodnotu řešení a jeho derivaci a nikoli hodnotu řešení ve dvou různých bodech. V některých případech to nevadí:
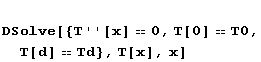
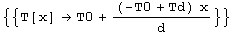
ndy to vadit bude. Každopádně jde o zajímavý vztah mezi PDR a ODR. Pojďme dále; často se uvádí rovnice uvažující přecházení tepla např. z vodiče do okolí konvekcí; pro plošnou hustotu výkonu platí q=a*(T[x]-Tokoli), dále se uvažuje
q*obvod*dx=Qv*průřez*dx; odtud snadno Qv=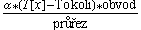 ; označme obvod=o, průřez=S
; označme obvod=o, průřez=S
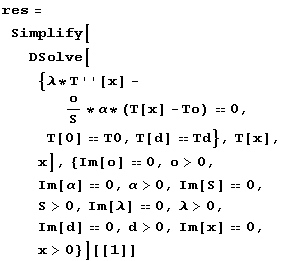
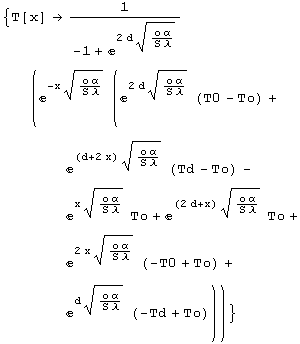


Na první pohled možná vypadá tento průběh podivně, ale když se nad tím zamyslíte, jak prostupuje teplo vedením třeba drátem a konvekcí do okolí /význam použitých symbolů je doufám jasný/, vidíme, že je to správně. Postupujme dále a vyšetřeme případy s proměnnými látkovými vlastnostmi, zde především tepelnou vodivostí. Styk dvou látek můžeme simulovat rychle probíhajícím spojitým přechodem.
Přílohy
| image15.gif |  |
1186 bytes |
| index_gr_1.gif |  |
1039 bytes |
| index_gr_10.gif |  |
169 bytes |
| index_gr_11.gif |  |
661 bytes |
| index_gr_12.gif |  |
277 bytes |
| index_gr_13.gif |  |
676 bytes |
| index_gr_14.gif |  |
1013 bytes |
| index_gr_16.gif |  |
662 bytes |
| index_gr_17.gif |  |
427 bytes |
| index_gr_19.gif |  |
2173 bytes |
| index_gr_2.gif |  |
682 bytes |
| index_gr_20.gif |  |
2307 bytes |
| index_gr_21.gif |  |
1392 bytes |
| index_gr_22.gif |  |
1007 bytes |
| index_gr_23.gif |  |
166 bytes |
| index_gr_24.gif |  |
2046 bytes |
| index_gr_25.gif |  |
1322 bytes |
| index_gr_26.gif |  |
166 bytes |
| index_gr_27.gif |  |
351 bytes |
| index_gr_28.gif |  |
887 bytes |
| index_gr_29.gif |  |
1443 bytes |
| index_gr_3.gif |  |
786 bytes |
| index_gr_30.gif |  |
1025 bytes |
| index_gr_31.gif |  |
166 bytes |
| index_gr_32.gif |  |
2242 bytes |
| index_gr_33.gif |  |
3402 bytes |
| index_gr_4.gif |  |
855 bytes |
| index_gr_6.gif |  |
309 bytes |
| index_gr_7.gif |  |
149 bytes |
| index_gr_8.gif |  |
849 bytes |
| index_gr_9.gif |  |
157 bytes |
| prvniet.nb |  |
136868 bytes |